Featured App

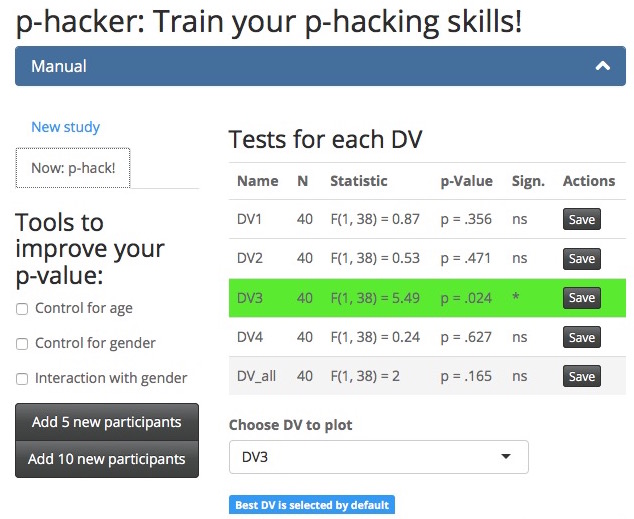
p-hacker: Train your p-hacking skills!

by Felix Schönbrodt
p-valuesteaching

Train your expert p-hacking skills with the interactive p-hacker app! Who gets p<.05 first?

Shiny widgets Experience statistics




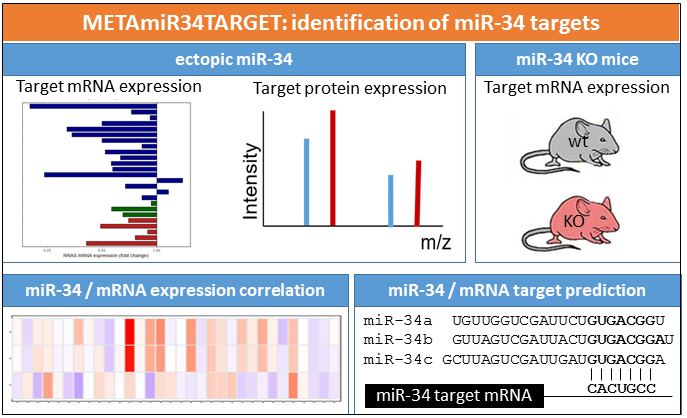
METAmiR34TARGET - Meta-analysis of microRNA-34 target mRNAs

by Matjaz Rokavec
Genome

This app allows to identify potential microRNA-34 targets by combining computational miRNA target prediction resources with experimental transcriptomic and proteomic datasets derived from cell lines, mouse models, and tumor tissues.

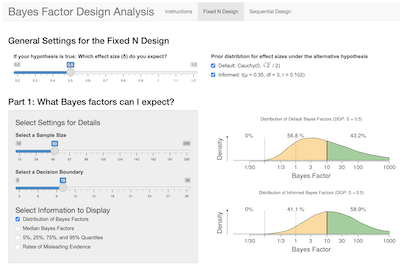
BFDA - A Shiny App for Bayesian Design Analysis

by Angelika Stefan
Bayes

This Shiny app helps researchers with sample size planning for Bayesian independent-samples t-tests, using Bayes Factor Design Analysis (BFDA), a simulation-based framework for Bayesian power analyses.

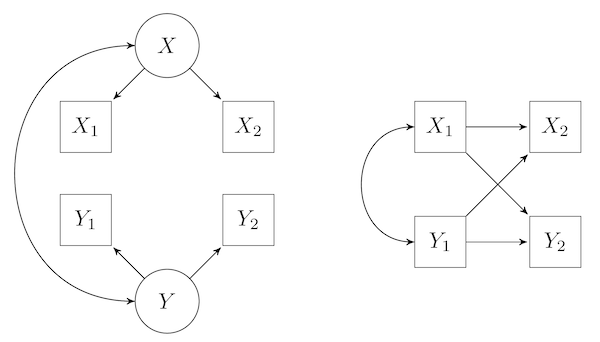
Examining the Effects of State and Trait Variance on Estimates of Cross-Lagged Associations

by Richard Lucas
SEM

This app generates 10 waves of data for two variables, based on a bivariate "stable trait, autoregressive trait, state" (STARTS) model and then runs a standard cross-lagged panel model, and a random-intercept cross-lagged panel model on the data. The purpose of the app is to examine how the estimated cross-lagged paths in the standard cross-lagged panel model and the random-intercept cross-lagged panel model are affected when stable-trait or state variance exists but is omitted from the model.

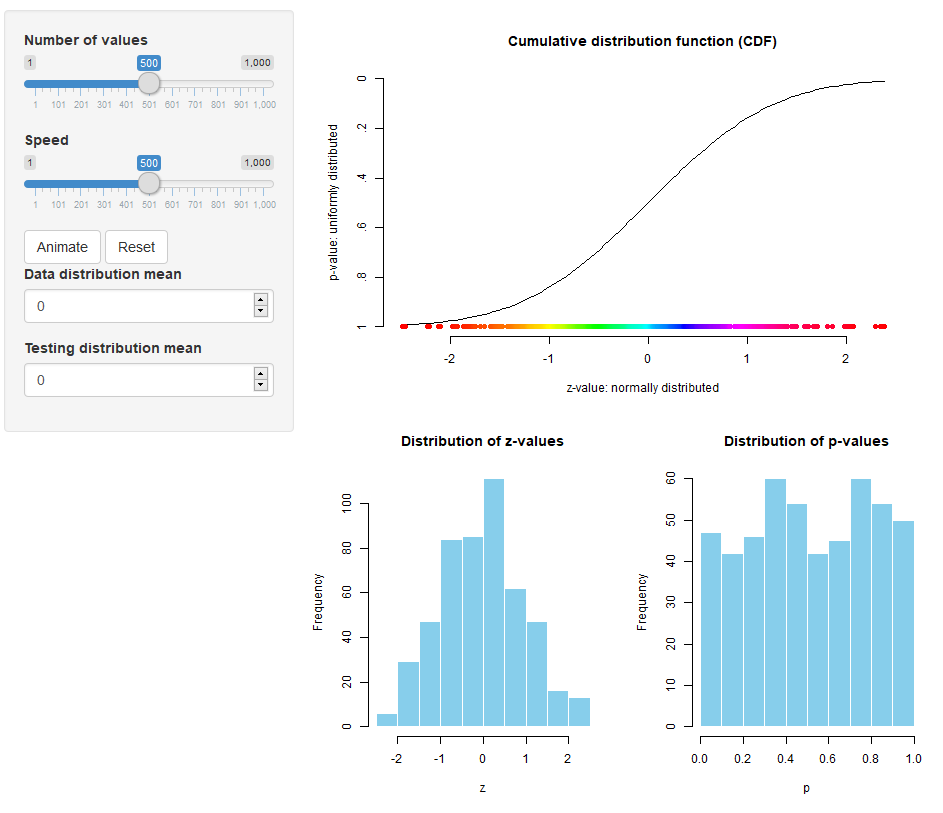
From z to p: A visualization of the link between the two distributions

by Sven Hilbert
p-valueplot

Ever wondered why p-values are uniformly distributed if the H0 is accurate, even though the data are normally distributed? This animated app visualizes the connection of the two via the CDF and lets you explore the relationship between effect size and skewness of the distribution of p-values.

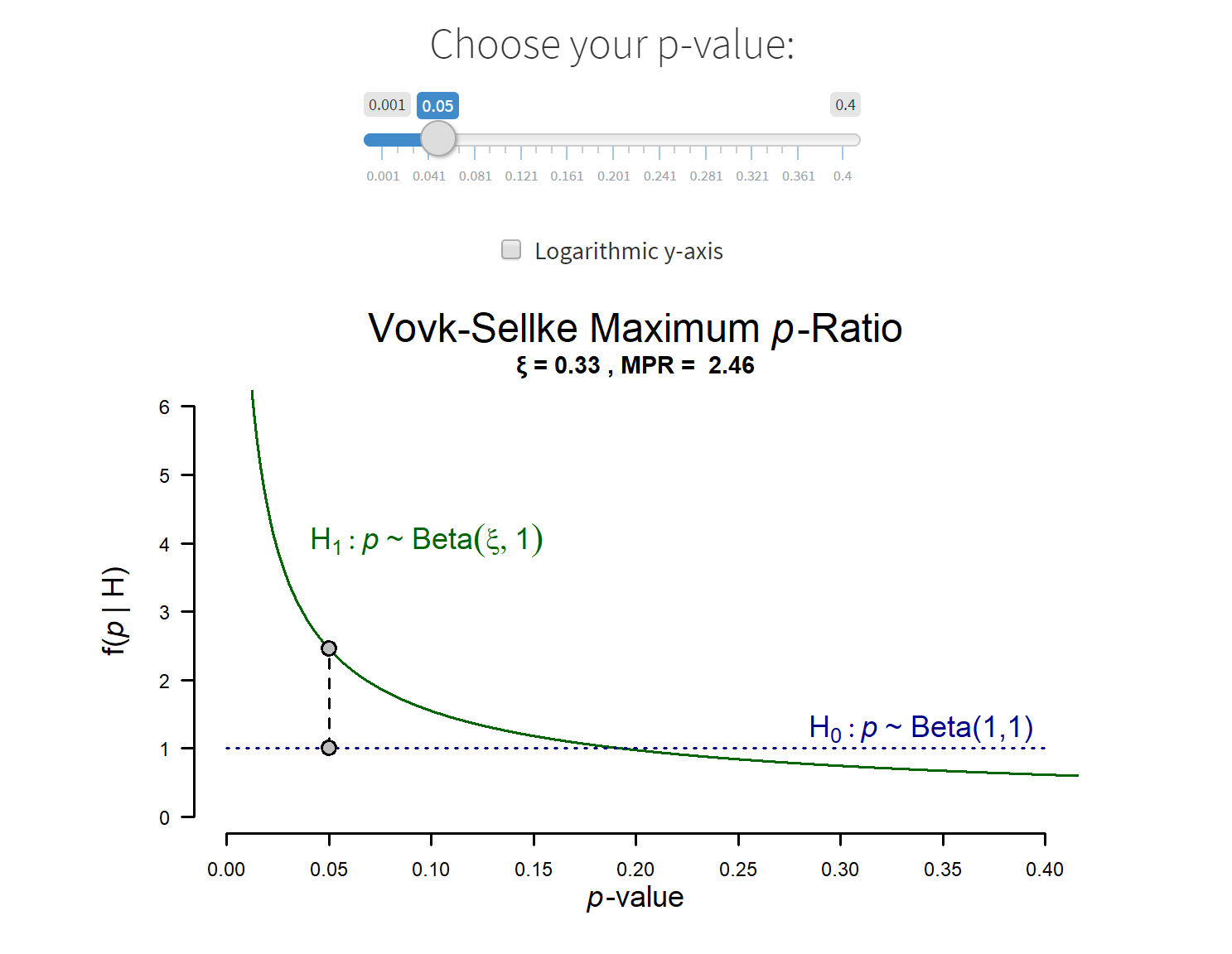
Exploring the diagnosticity of the p-value

by Erik-Jan van Kesteren and Eric-Jan Wagenmakers
p-valueplotdiagnosticity

Explore the Vovk-Sellke Maximum p-Ratio, a measure that indicates the maximum diagnosticity of a given p-value. Choose your own p-value to find out how diagnostic it is for your research!

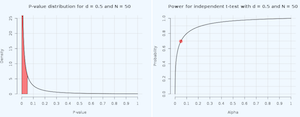
P-value distribution and power curves for an independent two-tailed t-test

by Daniel Lakens
p-valuepower

Plot the theoretical p-value distribution and power curve for an independent t-test based on the effect size, sample size, and alpha.

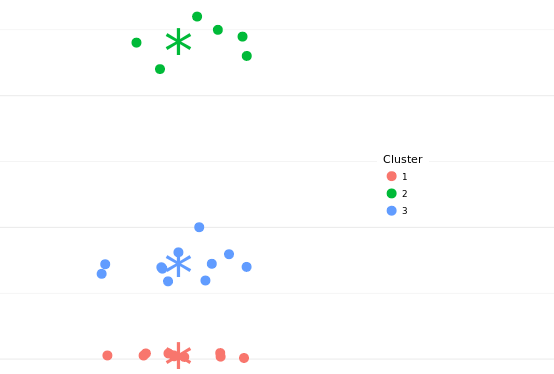
Univariate k-Means Clustering with elbow method

by Jan Freyberg
clustering

Identify how many clusters your one-dimensional data can be grouped in and how much variance you can explain with these clusters by using the "elbow method".

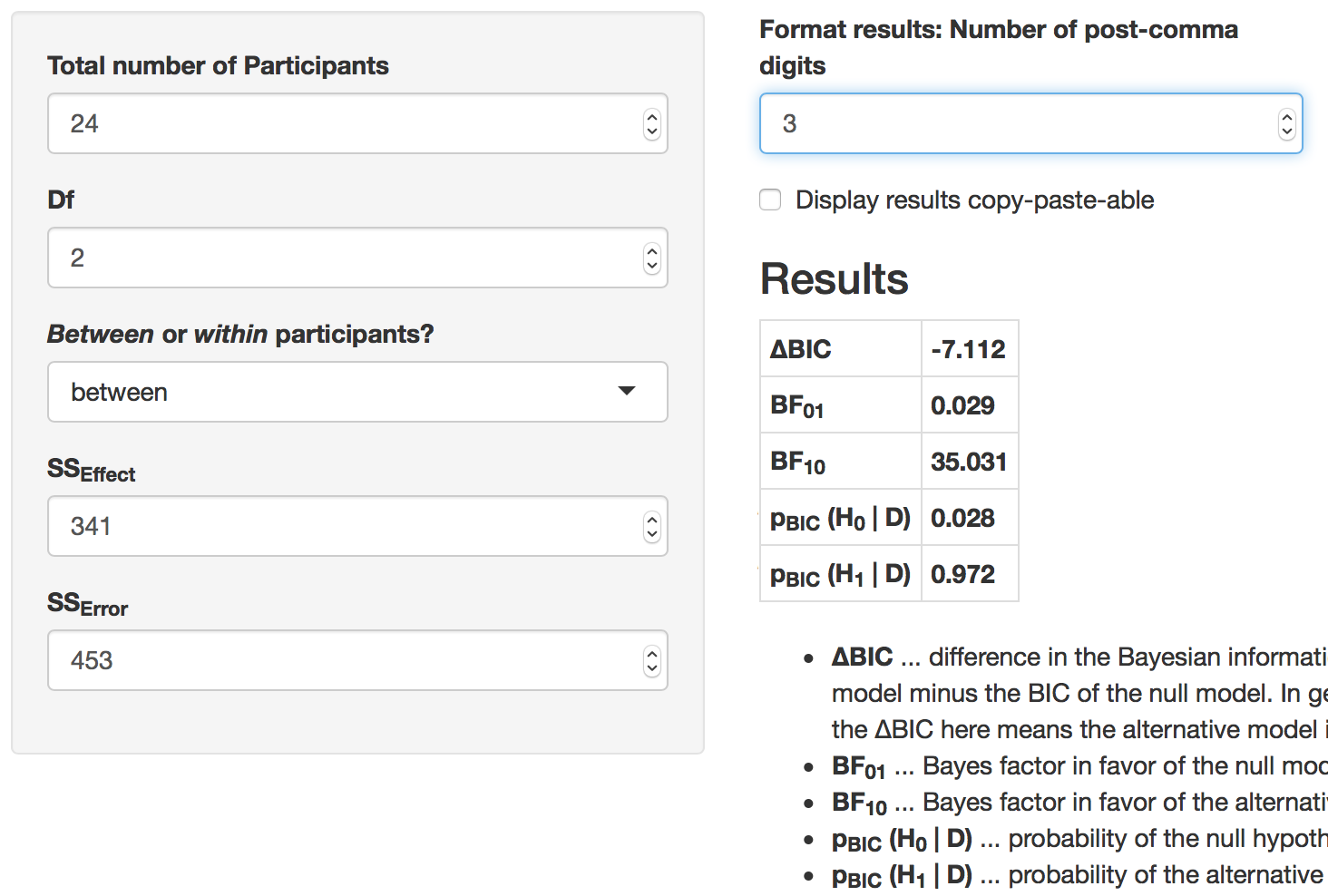
BIC approximation for ANOVA designs

by Christoph Huber-Huber
Bayes

Obtain a Bayesian interpretation of your ANOVA results with this app. You just need to enter your sum of squares and some information about your design.

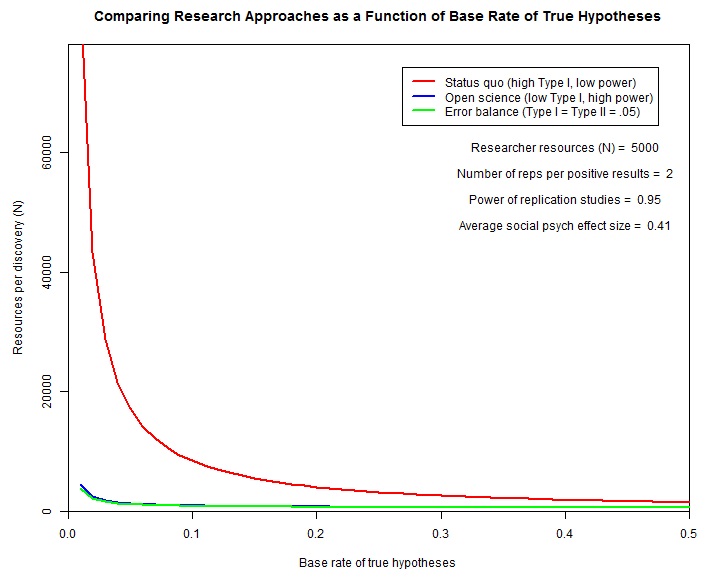
N per discovery

by Etienne LeBel
paper

App to explore the cost-effectiveness of different research approaches to unearth true scientific discoveries.

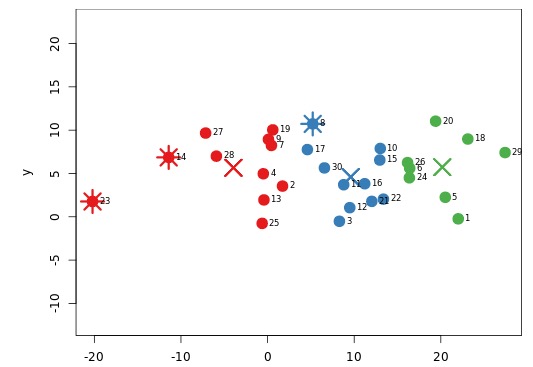
2D Outlier analysis

by Rajiv Shah
outlier

The app allows you to see the trade-offs on various types of outlier/anomaly detection algorithms. Outliers are marked with a star and cluster centers with an X.

When does a significant p-value indicate a true effect?

by Michael Zehetleitner and Felix Schönbrodt
teaching

Understanding the Positive Predictive Value (PPV) of a p-value.

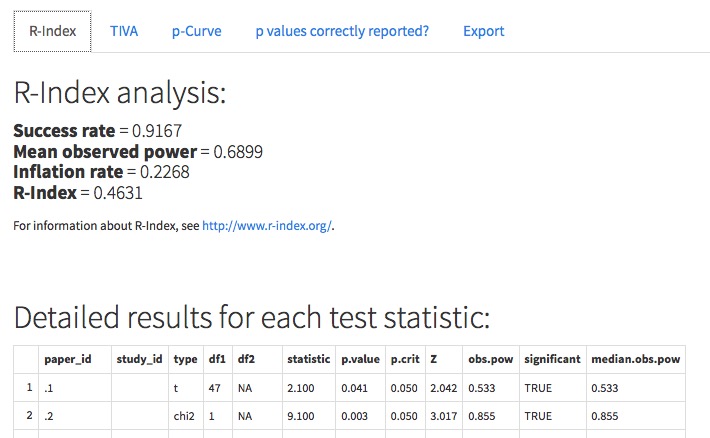
p-checker: The one-for-all p-value analyzer

by Felix Schönbrodt
p-value

This Shiny app implements the p-curve (Simonsohn, Nelson, & Simmons, 2014; see http://www.p-curve.com) in its previous ("app2") and the current version ("app3"), the R-Index and the Test of Insufficient Variance, TIVA (Schimmack, 2014; see http://www.r-index.org/), and tests whether p values are reported correctly.

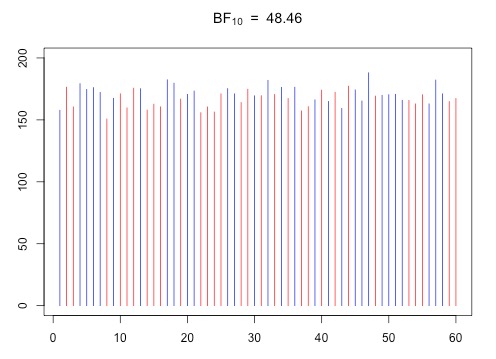
What does a Bayes factor look like? (2) Height difference between males and females.

by Felix Schönbrodt
Bayesteaching

Can you "see" a group mean difference, just by eyeballing the data? Is your gut feeling aligned to the formal index of evidence, the Bayes factor?

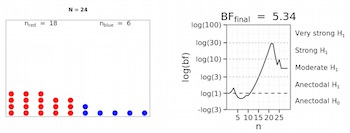
What does a Bayes factor look like? (1) The urn model.

by Felix Schönbrodt
Bayesteaching

How much is a BF of 3.7? Well, it is "moderate evidence" for an effect - whatever that means. Let's approach the topic a bit more experientially. What does such a BF look like, visually? We take the good old urn model as an example.

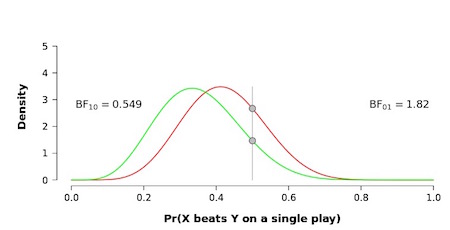
A First Lesson in Bayesian Inference

by Eric-Jan Wagenmakers
Bayes

This app highlights several key Bayesian concepts.

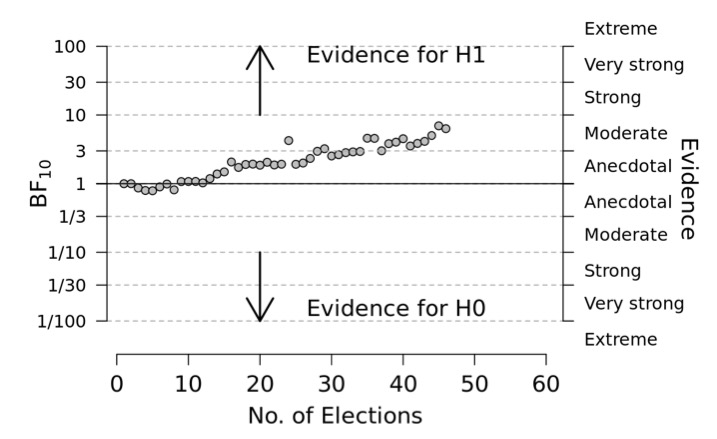
A Compendium of Clean Graphs in R

by Eric-Jan Wagenmakers
Bayesplot

When done right, graphs can be appealing, informative, and of considerable value to an academic article. This compendium facilitates the creation of good graphs by presenting a set of concrete examples, ranging from the trivial to the advanced. The graphs can all be reproduced and adjusted by copy-pasting code into the R console.

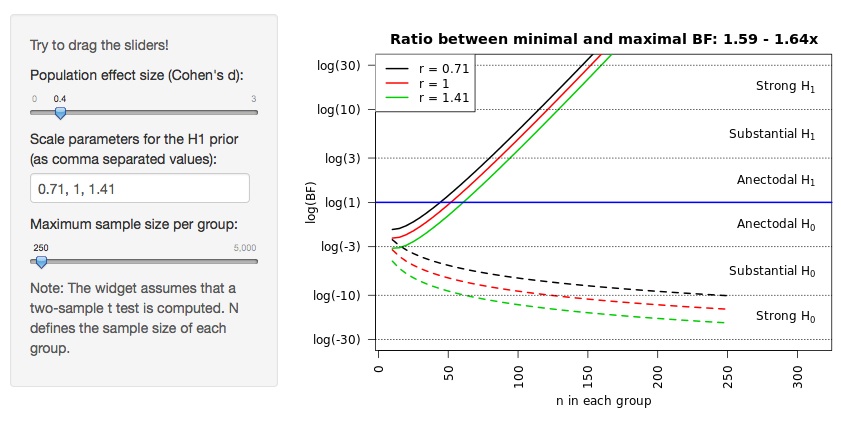
Bayes factor robustness

by Felix Schönbrodt
Bayesplot

Check how your Bayes factor conclusion depends on the r-scale parameter.

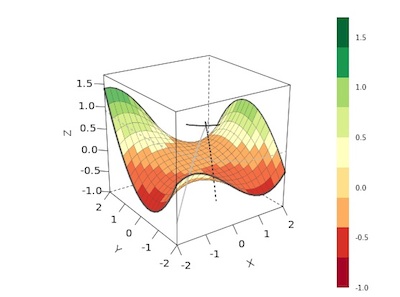
Polynomial Surface Explorer

by Felix Schönbrodt
regressionplot

Adjust regression parameters to bend and shift a two-dimensional polynomial surface.

Find-a-fit!

by Felix Schönbrodt
regressionplotgame

Be an optimizer: Find the best linear fit!

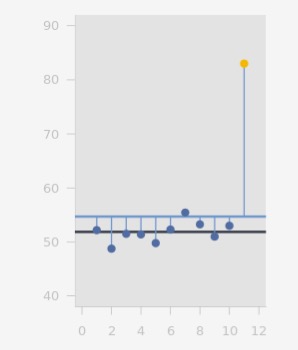
Robustness of Mean and Median

by Tobias Kächele
quiz

Which is more robust against outliers: Mean or median?

Normal distribution vs. binomial

by Tobias Kächele
quizdistribution

Approximating a normal distribution with a binomial distribution

Production errors

by Tobias Kächele
quizhistogramdistribution

Get acquainted with histograms.